Mitkä ovat binaarihakupuun pahin tapaus ja keskimääräinen tapausten monimutkaisuus?

Video: Mitkä ovat binaarihakupuun pahin tapaus ja keskimääräinen tapausten monimutkaisuus?

2024 Kirjoittaja: Lynn Donovan | [email protected]. Viimeksi muokattu: 2023-12-15 23:46

Binäärihakupuu

Algoritmi	Keskiverto	Pahimmassa tapauksessa
Avaruus	Päällä)	Päällä)
Hae	O(log n)	Päällä)
Lisää	O(log n)	Päällä)
Poistaa	O(log n)	Päällä)

Sitä paitsi, mikä on binaarihakupuun suuri O pahimman tapauksen aika monimutkaisuus?

A:n rekursiivinen rakenne BST tuottaa rekursiivisen algoritmin. Etsitään jonkin sisällä BST on O (h) pahin - tapaus suoritusaika monimutkaisuus , jossa h on korkeus puu . Koska s binäärihakupuu n solmulla on vähintään O (log n) tasot, se kestää vähintään O (log n) vertailut tietyn solmun löytämiseksi.

Toiseksi, mikä on iteroinnin kanssa tehtävän binäärihaun aikamonimutkaisuus? Suoritus Binäärihakualgoritmi : Siksi, binäärihakualgoritmin aika monimutkaisuus on O(log₂n) joka on erittäin tehokas. Sen käyttämä aputila on O(1) for iteratiivinen toteutus ja O(log₂n) rekursiiviseen toteutukseen kutsupinon takia.

Kysymys kuuluu myös, mikä olisi binäärihakupuun elementin etsimisen pahimman mahdollisen ajan monimutkaisuus?

Aika monimutkaisuus : pahimmassa tapauksessa aika monimutkaisuus / Hae ja lisäysoperaatiot on O(h), missä h on korkeus Binäärihakupuu . Sisään Pahimmassa tapauksessa , me saattaa omistaa to matkustaa juuresta to syvin lehtisolmu. Vinon korkeus puu voi muuttuvat n:ksi ja aika monimutkaisuus / Hae ja aseta toiminto saattaa muuttuu O(n).

Onko Big O pahin tapaus?

Joten binäärihaussa paras tapaus On O (1), keskiarvo ja Pahimmassa tapauksessa On O (kirjaudu sisään). Lyhyesti sanottuna ei ole olemassa minkäänlaista suhdetta iso o käytetään Pahimmassa tapauksessa , Theta keskimäärin tapaus ”. Kaikentyyppisiä merkintöjä voidaan käyttää (ja joskus käytetään) puhuttaessa parhaasta, keskimääräisestä tai Pahimmassa tapauksessa algoritmista.

Suositeltava:

Mitä eroa on tapausten hallinnan ja suurten tapausten hallinnan välillä?

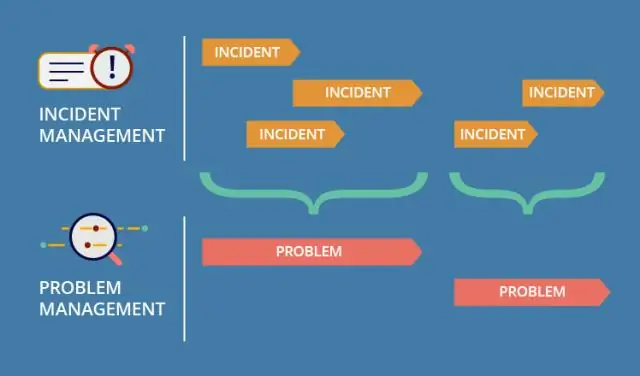
Joten MI tarkoittaa sen tunnustamista, että normaali tapausten ja ongelmien hallinta eivät aio leikata sitä. Suuronnettomuus on hätätilan julistaminen. Suuri tapaus on tavallisen tapahtuman ja katastrofin puolivälissä (jossa IT-palvelun jatkuvuuden hallintaprosessi käynnistyy)

Mikä on termiittiteltan keskimääräinen hinta?

Keskimääräiset kustannukset talon telttauksesta termiittikaasutusta varten ovat 1 280–3 000 dollaria tai 1–4 dollaria neliöjalkaa kohden tartunnan tasosta riippuen. Toinen vaihtoehto koko kodille on lämpökäsittely, joka maksaa yleensä 1–2,50 dollaria neliöjalkaa kohti, ja useimmat asunnonomistajat maksavat noin 800–2 800 dollaria

Kuinka toteutat binaarihakupuun Javassa?

Binaarihakupuun (BST) toteuttaminen Javassa Solmun vasemmassa alipuussa on vain solmuja, joiden avaimet ovat pienempiä kuin solmun avain. Solmun oikea alipuu sisältää vain solmuja, joiden avaimet ovat suuremmat kuin solmun avain. Vasemman ja oikean alipuun on oltava myös binäärihakupuu. Ei saa olla päällekkäisiä solmuja

Mikä on keskimääräinen jonon pituus?

Yleensä keskimääräinen jonon pituus (tai keskimääräinen asiakkaiden määrä järjestelmässä) on yhtä suuri kuin: N = keskimääräinen (odotettu) asiakkaiden lukumäärä = 0 × Ҏ[k asiakasta järjestelmässä] + 1 × Ҏ[1 asiakas järjestelmässä] + 2 × Ҏ[2 asiakasta järjestelmässä] +. =