Video: Mitä eroa on deduktiivisen ja ampliatiivisen argumentin välillä?
2024 Kirjoittaja: Lynn Donovan | [email protected]. Viimeksi muokattu: 2023-12-15 23:46
Jos väittelijä uskoo, että premissien totuus vahvistaa johtopäätöksen totuuden, niin Perustelu On deduktiivinen . Jos väittelijä uskoo, että premissien totuus antaa vain hyviä syitä uskoa, että johtopäätös on todennäköisesti totta, niin Perustelu On induktiivinen.
Tästä syystä, mikä on ampliatiivinen argumentti?
Nopea viittaus. Peircen käyttämä termi kuvaamaan argumentteja joiden johtopäätökset menevät heidän lähtökohtiensa ulkopuolelle (ja siten vahvistavat uskomuksemme laajuutta). Induktiivinen argumentteja ja argumentteja parhaalla mahdollisella tavalla eivät ole deduktiivisesti päteviä, mutta voivat antaa uskottavia johtopäätöksiä.
Edellä olevan lisäksi, mikä on hyvä deduktiivinen argumentti? A hyvä deduktiivinen argumentti todella[br]takaa sen johtopäätöksen. Osa siitä, mitä tämä tarkoittaa, on, että on mahdotonta, että premissit ovat tosia, kun taas johtopäätös on väärä. Kun näin on, sanomme, että [br] Perustelu on voimassa.
Lisäksi mikä on tärkein ero deduktiivisten ja induktiivisten argumenttien välillä?
Tarkkuus induktiivinen päättely on kyseenalainen. Koska induktiivinen päättely käyttää tiettyjä premissioita johtopäätöksen tekemiseen, johtopäätös on todennäköinen, mutta ei täysin totta. Deduktiivinen päättely voi johtaa ehdottoman oikeaan johtopäätökseen, jos ja vain, jos siihen johtopäätökseen johtavat premissit ovat myös tosia.
Mikä on esimerkki pätevästä deduktiivisesta argumentista?
Sisään deduktiivinen argumentti , varten esimerkki saamme tämän: kaikki poikamiehet ovat naimattomia. Käsityksemme perusteella poikamiehestä seuraa, että he ovat naimattomia. Toinen esimerkki on: Pietari on kuolevainen, Pietari on ihminen, joten Pietari on kuolevainen. Huomaa: tilojesi on tuettava täysin päätelmääsi.
Suositeltava:
Mitä eroa on Pebble Tecin ja Pebble Sheenin välillä?
Pebble Tec on valmistettu luonnollisista, kiillotetuista kivistä, jotka luovat kuoppaisen ja liukumattoman pinnan. Pebble Sheen käyttää samaa tekniikkaa kuin Pebble Tec, mutta käyttää pienempiä kiviä liukkaamman viimeistelyn saamiseksi
Mitä eroa on kognitiivisen psykologin ja kognitiivisen neurotieteilijän välillä?
Kognitiivinen psykologia keskittyy enemmän tiedonkäsittelyyn ja käyttäytymiseen. Kognitiivinen neurotiede tutkii tiedonkäsittelyn ja käyttäytymisen taustalla olevaa biologiaa. kognitiivinen neurotiede keskellä
Mitä eroa on kokoamisen ja purkamisen välillä?
On, että kokoonpano on (laskeminen) Microsoft netissä, sovelluksen rakennuspalikka, joka on samanlainen kuin dll, mutta sisältää sekä suoritettavan koodin että dll-tyyppikirjastossa tavallisesti löytyvän tiedon. Kokoonpanon tyyppikirjaston tiedot, joita kutsutaan manifestiksi, kuvaavat julkiset toiminnot, tiedot, luokat ja versiot
Mitä ovat Toulmin-argumentin tarkenteet?
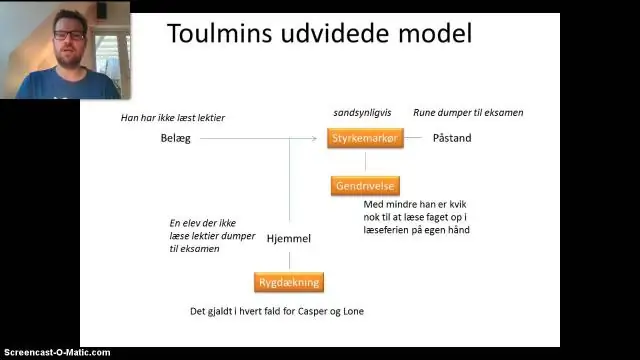
Tarkenne (tai modaalinen tarkenne) osoittaa harppauksen voimakkuuden tiedoista warrantiin ja voi rajoittaa sitä, kuinka yleinen vaatimus koskee. Ne sisältävät sanoja, kuten "usein", "yleensä", "aina" tai "joskus"
Mitä eroa on induktiivisen argumentin ja deduktiivisen argumentin välillä?
Deduktiivisilla argumenteilla on kiistattomia johtopäätöksiä olettaen, että kaikki premissit ovat tosia, mutta induktiivisilla argumenteilla on yksinkertaisesti jonkin verran todennäköisyyttä, että argumentti on totta – argumentin vahvuuden ja sitä tukevien todisteiden perusteella