
Sisällysluettelo:
- Kirjoittaja Lynn Donovan [email protected].
- Public 2023-12-15 23:46.
- Viimeksi muokattu 2025-01-22 17:23.
Yhdistä lajittelu
- Jaa lajittelematon luettelo alaluetteloihin, joista jokainen sisältää elementin.
- Otetaan vierekkäiset kahden singleton listan parit ja yhdistää ne muodostavat luettelon 2 elementistä. N. muuntaa nyt koon 2 listoiksi.
- Toista prosessi yhdeksi lajiteltu lista hankituista.
Tiedätkö myös, mikä on yhdistäminen esimerkin kanssa?
An esimerkki / Yhdistä lajittelu . Jaa luettelo ensin pienimpään yksikköön (1 elementti) ja vertaa sitten jokaista elementtiä viereiseen luetteloon järjestellä ja yhdistää kaksi vierekkäistä listaa. Lopulta kaikki elementit ovat lajiteltu ja yhdistetty . Yhdistä lajittelu on hajota ja hallitse -algoritmi, jonka John von Neumann keksi vuonna 1945.
Samoin missä yhdistämislajittelua käytetään? Sovellukset Yhdistä lajittelu Yhdistä lajittelu on hyödyllinen lajittelu linkitetyt listat O(nLogn)-ajassa. Linkitettyjen listojen tapauksessa tapaus on erilainen pääasiassa taulukoiden ja linkitettyjen luetteloiden muistin varauksen eron vuoksi. Toisin kuin taulukot, linkitetyt luettelosolmut eivät välttämättä ole vierekkäin muistissa.
On myös tiedettävä, mikä on yhdistämislajittelu ja miten se toimii?
Yhdistä lajittelu on hajota ja hallitse -algoritmi. Se toimii jakamalla ongelman rekursiivisesti kahteen tai useampaan saman tai samantyyppiseen osaongelmaan, kunnes niistä tulee tarpeeksi yksinkertaisia, jotta ne voidaan ratkaista suoraan. Niin Yhdistä lajittelu jakaa ensin taulukon yhtä suureen osaan ja sitten yhdistävät ne a lajiteltu tavalla.
Mitä tarkoittaa yhdistämislajittelu?
Yhdistä lajittelu . (algoritmi) Määritelmä : A järjestellä Algoritmi, joka jakaa kohteet oleviksi lajiteltu kahteen ryhmään, rekursiivisesti lajittelee jokainen ryhmä ja sulautuu ne finaaliin, lajiteltu järjestys. Ajoaika on Θ(n log n).
Suositeltava:
Kuinka kirjoitat shell-komentoja?

Mikä on Shell-komentosarja? Luo tiedosto vi-editorilla (tai millä tahansa muulla editorilla). Nimeä komentosarjatiedosto, jonka laajennus.sh. Aloita käsikirjoitus #! /bin/sh. Kirjoita joku koodi. Tallenna komentosarjatiedosto nimellä tiedostonimi.sh. Skriptin suorittamiseen kirjoita bash filename.sh
Kuinka kirjoitat F-merkkijonon Pythonissa?

Jos haluat luoda f-merkkijonon, liitä sen eteen kirjain " f ". Itse merkkijono voidaan muotoilla samalla tavalla kuin str. muoto(). F-merkkijonot tarjoavat tiiviin ja kätevän tavan upottaa python-lausekkeita merkkijonoliteraaleihin muotoilua varten
Kuinka kirjoitat BAPI:n SAP:ssa?
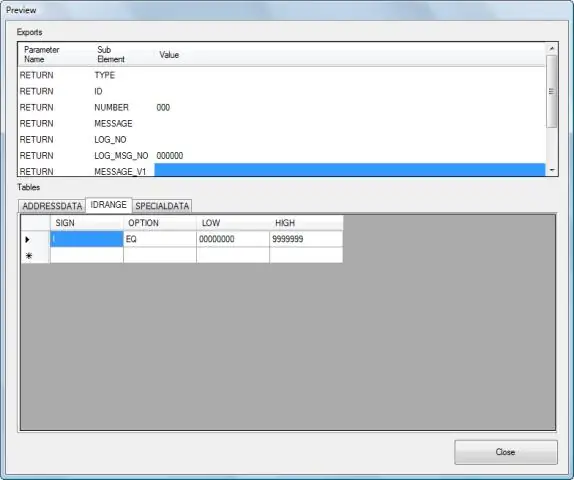
Luo mukautettu BAPI noudattamalla alla olevia ohjeita. Luo SE11:ssä rakenteita parametrien tuontia ja vientiä varten. Luo etäkäyttöinen toimintomoduuli, jossa on tuonti- ja vientiparametreja (täytyy olla tyyppirakennetta) SE37:ssä. Luo liiketoimintaobjekti SWO1:ssä. Lisää RFC-funktiomoduuli liiketoimintaobjektiin
Miten yhdistämislajittelun monimutkaisuus lasketaan?
2 vastausta. Solmun A[L,R] jakaminen kahdeksi solmuksi kestää R&miinus L+1 ajan ja sitten kahden lapsisolmun A[L,M] ja A[M+1,R] yhdistäminen vie taas A[R&miinus; +1] kertaa. Siten jokaiselle solmulle algoritmin suorittamien operaatioiden määrä on kaksi kertaa sitä solmua vastaavan taulukon koko
Mikä on yhdistämislajittelun paras tapausaikainen monimutkaisuus?

Lajittelualgoritmit Algoritmi Tietorakenne Tilan monimutkaisuus: Huonoin pikalajittelu Joukko O(n) Yhdistä lajittelu Taulukko O(n) Keon lajittelu Taulukko O(1) Tasainen lajittelu Joukko O(1)
